初中数学中经常会遇到一类几何题,证明三条线段长度的“和”或"差”及其比例关系,或者是给出这样的条件让我们求某些结论。这类题目一般采取“截长”或“补短”的方法来进行求解。
“截长”是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系。
“补短”,是将一个已知的较短的线段延长至与另一个已知的较短的长度相等,然后求出延长后的线段与最长的已知线段的关系。
采取截长补短法后,使之构成全等或其他特殊的三角形求解。
【例题1】已知:△ABC中,AB=AC,D为△ABC外一点,且∠ABD=60°,∠ADB=90°-1/2∠BDC,试判断线段CD、BD与AB之间有怎样的数量关系?
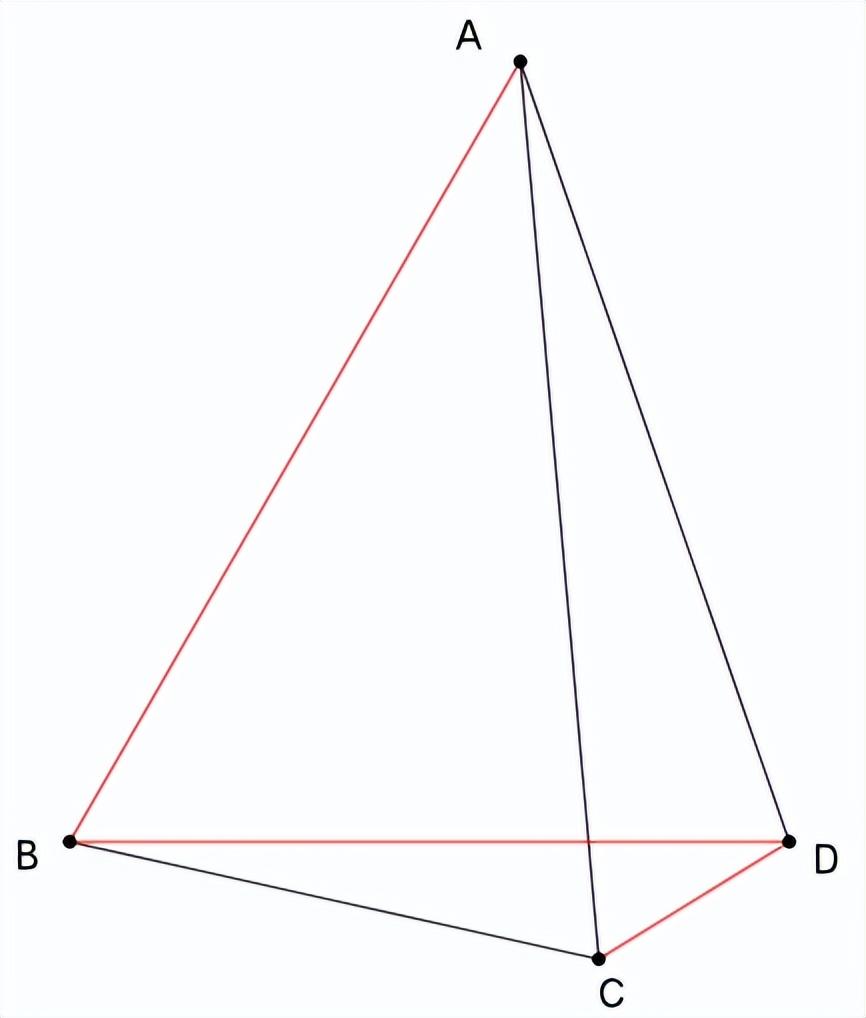
分析:三条线段CD、BD与AB之间的数量关系,往往是两条线段长度的和等于另外一条线段的长度。
题目中给出三条线段之间或者求三条线段之间的数量关系,一般采用截长补短法,构造全等三角形求解。
延长CD到E,使DE=BD,连接AE
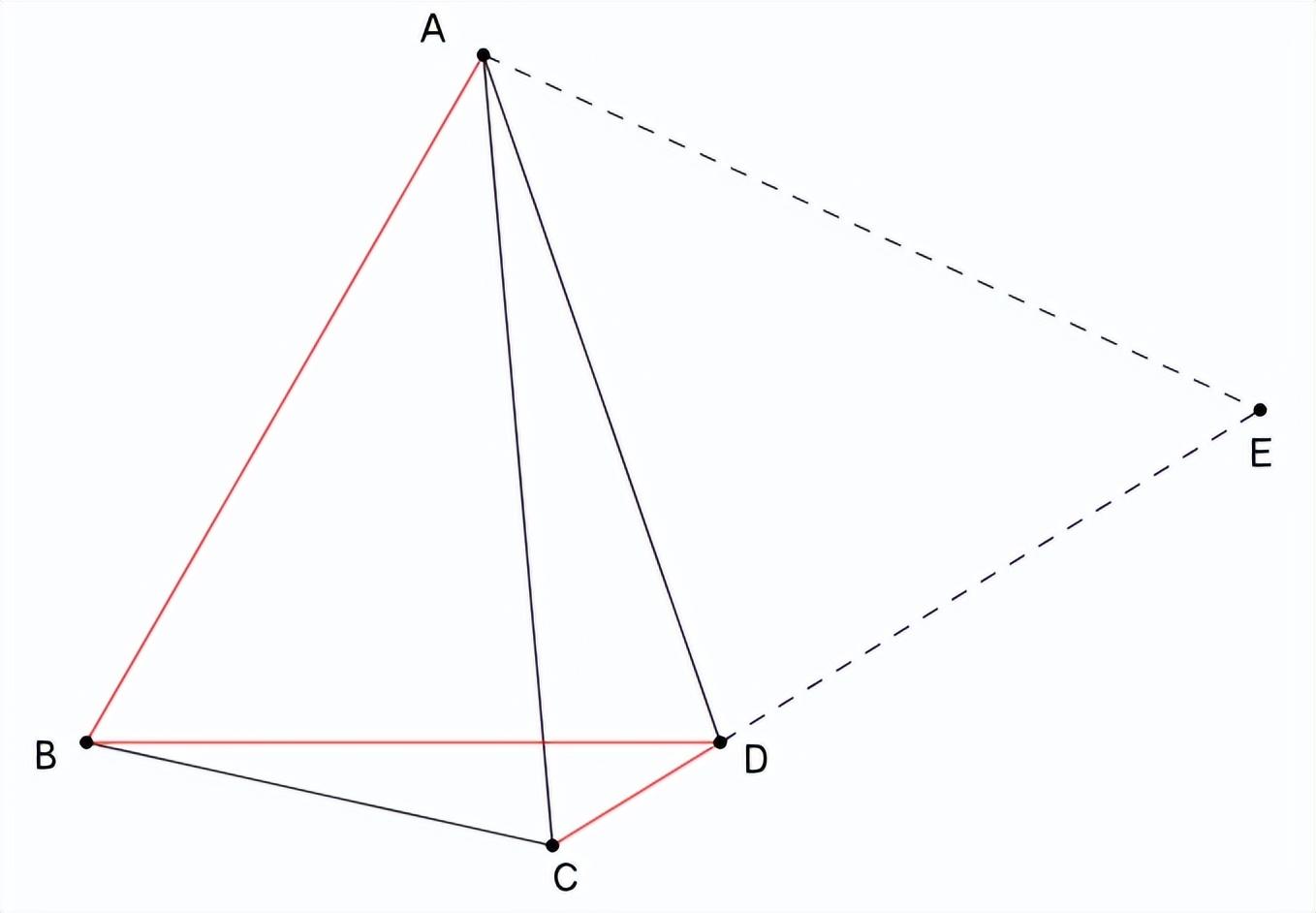
CE=CD+DE=CD+BD
看图中所示,在△ABD和△AED中,
AD=AD
BD=DE
∠ADB=90°-1/2∠BDC
那么∠ADE呢?
所以,△ABD≌△AED(SAS)
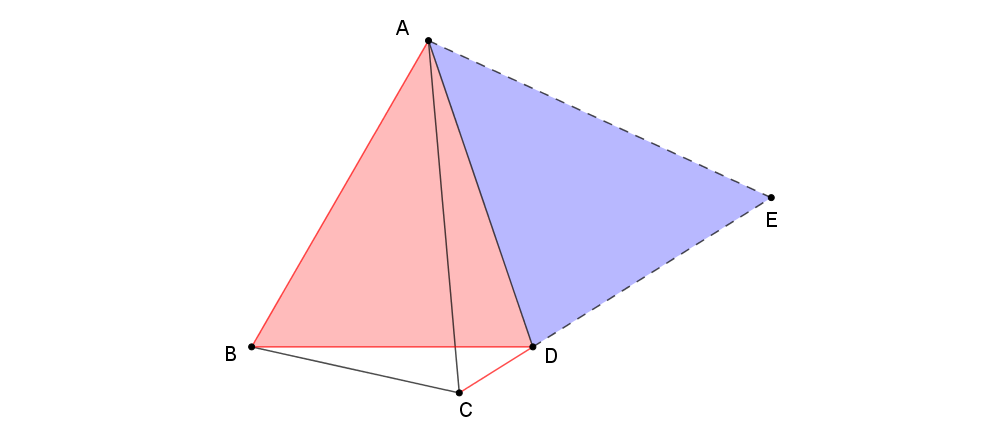
AB=AE=AC,
三角形ACE是等腰三角形。
因为∠AED=∠ABD=60°,
所以三角形ACE是等边三角形。
我们就能得到
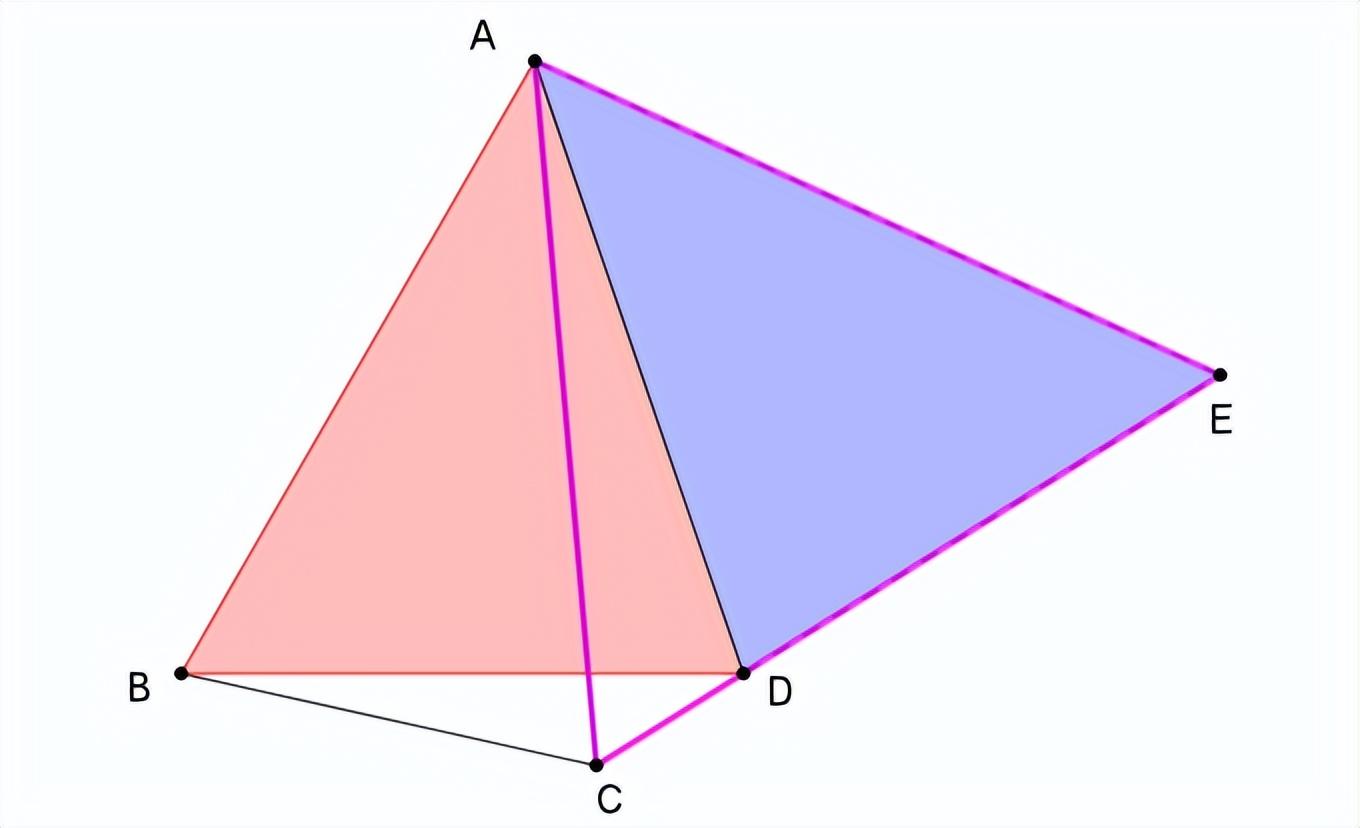
CE=AC=AB
所以,AB=CD+BD
线段CD、BD与AB之间的数量关系为AB=CD+BD。
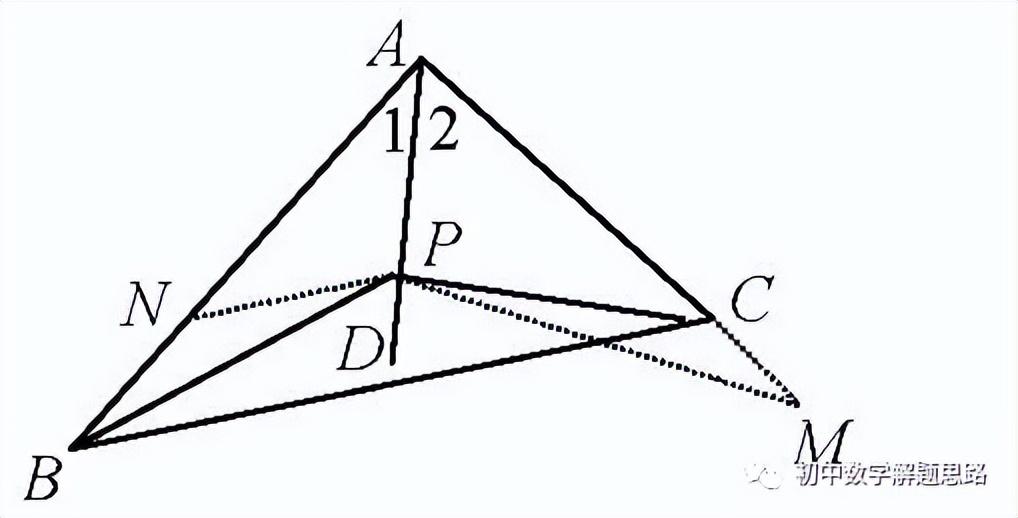
【例题2】已知如图:在△ABC 中,AB>AC,∠1=∠2,P 为AD 上任一点,
求证:AB-AC>PB-PC.
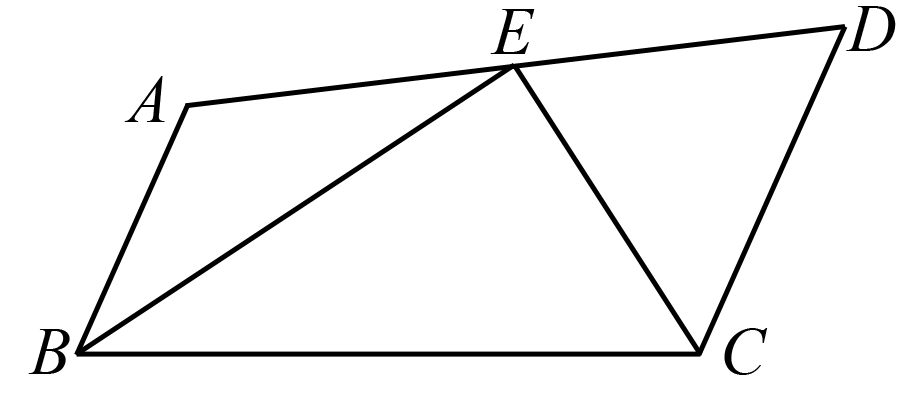
练习.如图,AB∥CD,CE、BE分别平分∠BCD和∠CBA,点E在AD上,求证:BC=AB+CD.
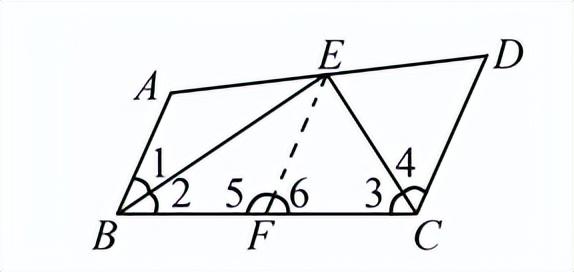
证明:在BC上取一点F,使BF=BA,连接EF.在△ABE和△FBE中,BE=BE(∠1=∠2),∴△ABE≌△FBE(SAS).
∴∠A=∠5.∵AB∥CD,∴∠A+∠D=180°,而∠5+∠6=180°,∴∠6=∠D.在△EFC和△EDC中,CE=CE(∠3=∠4),∴△EFC≌△EDC(AAS),∴FC=DC.∴BC=BF+CF=AB+CD.
总之,当已知条件出现线段之间的关系,或者是求证线段之间的关系,这个时候就可以使用截长补短的方法。
